1. 引言

LZ77算法是采用字典做数据压缩的算法，由以色列的两位大神Jacob Ziv与Abraham Lempel在1977年发表的论文《A Universal Algorithm for Sequential Data Compression》中提出。

基于统计的数据压缩编码，比如Huffman编码，需要得到先验知识——信源的字符频率，然后进行压缩。但是在大多数情况下，这种先验知识是很难预先获得。因此，设计一种更为通用的数据压缩编码显得尤为重要。LZ77数据压缩算法应运而生，其核心思想：利用数据的重复结构信息来进行数据压缩。举个简单的例子，比如

取之以仁义，守之以仁义者，周也。取之以诈力，守之以诈力者，秦也。

取之以、仁义、，、者、守之以、也、诈力、。均重复出现过，只需指出其之前出现的位置，便可表示这些词。为了指明出现位置，我们定义一个相对位置，如图

相对位置之后的消息串为取之以诈力，守之以诈力者，秦也。，若能匹配相对位置之前的消息串，则编码为以其匹配的消息串的起始与末端index；若未能匹配上，则以原字符编码。相对位置之后的消息串可编码为：[(1-3),(诈力),(6),(7-9),(诈力),(12),(6),(秦),(15-16)]，如图所示：

上面的例子展示如何利用索引值来表示词，以达到数据压缩的目的。LZ77算法的核心思想亦是如此，其具体的压缩过程不过比上述例子稍显复杂而已。

2. 原理

本文讲主要讨论LZ77算法如何做压缩及解压缩，关于LZ77算法的唯一可译、无损压缩（即解压可以不丢失地还原信息）的性质，其数学证明参看原论文[1]。

滑动窗口

至于如何描述重复结构信息，LZ77算法给出了更为确切的数学解释。首先，定义字符串\(S\)的长度为\(N\)，字符串\(S\)的子串\(S_{i,j},\ 1\le i,j \le N\)。对于前缀子串\(S_{1,j}\)，记\(L_i^j\)为首字符\(S_{i}\)的子串与首字符\(S_{j+1}\)的子串最大匹配的长度，即：

\[ L_i^j = \max \{ l | S_{i,i+l-1} = S_{j+1,j+l} \} \quad \text{subject to} \quad l \le N-j \]

我们称字符串\(S_{j+1,j+l}\)匹配了字符串\(S_{i,i+l-1}\)，且匹配长度为\(l\)。如图所示，存在两类情况：

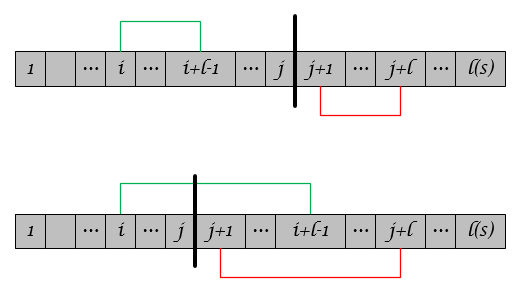
定义\(p^j\)为所有情况下的最长匹配的\(i\)值，即

\[ p^j = \mathop {\arg \max }\limits_{i} \{ L_i^j \} \quad \text{subject to} \quad 1 \le i \le j \]

比如，字符串\(S=00101011\)且\(j=3\)，则有

• \(L_1^j=1\)，因为\(S_{j+1,j+1}=S_{1,1}\), \(S_{j+1,j+2} \ne S_{1,2}\);
• \(L_2^j=4\)，因为\(S_{j+1,j+1}=S_{2,2}\), \(S_{j+1,j+2} = S_{2,3}\)，\(S_{j+1,j+3} = S_{2,4}\)，\(S_{j+1,j+4} = S_{2,5}\)，\(S_{j+1,j+5} \ne S_{2,6}\)；
• \(L_3^j = 0\)，因为\(S_{j+1,j+1} \ne S_{3,3}\)。

因此，\(p^j = 2\)且最长匹配的长度\(l^j=4\). 从上面的例子中可以看出：子串\(S_{j+1,j+p}\)是可以由\(S_{1,j}\)生成，因而称之为\(S_{1,j}\)的再生扩展（reproducible extension）。LZ77算法的核心思想便源于此——用历史出现过的字符串做词典，编码未来出现的字符，以达到数据压缩的目的。在具体实现中，用滑动窗口（Sliding Window）字典存储历史字符，Lookahead Buffer存储待压缩的字符，Cursor作为两者之间的分隔，如图所示：

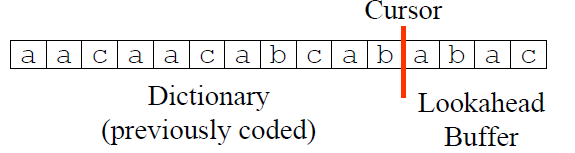
并且字典与Lookahead Buffer的长度是固定的。

压缩

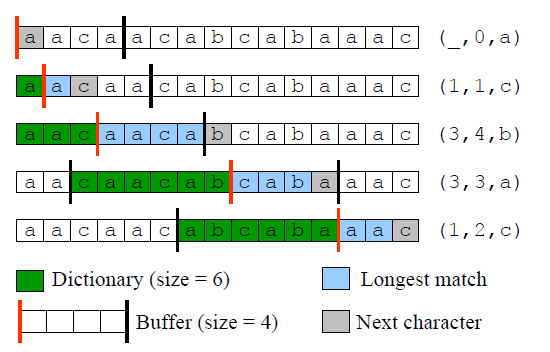
用\((p,l,c)\)表示Lookahead Buffer中字符串的最长匹配结果，其中

• \(p\)表示最长匹配时，字典中字符开始时的位置（相对于Cursor位置），
• \(l\)为最长匹配字符串的长度，
• \(c\)指Lookahead Buffer最长匹配结束时的下一字符

压缩的过程，就是重复输出\((p,l,c)\)，并将Cursor移动至\(l+1\)，伪代码如下：

Repeat:    Output (p,l,c),    Cursor --> l+1Until to the end of string

压缩示例如图所示：

解压缩

为了能保证正确解码，解压缩时的滑动窗口长度与压缩时一样。在解压缩，遇到\((p,l,c)\)大致分为三类情况：

• \(p==0\)且\(l==0\)，即初始情况，直接解码\(c\)；
• \(p>=l\)，解码为字典dict[p:p+l+1]；
• \(p<l\)，即出现循环编码，需要从左至右循环拼接，伪代码如下：

for(i = p, k = 0; k < length; i++, k++)    out[cursor+k] = dict[i%cursor]

比如，dict=abcd，编码为(2,9,e)，则解压缩为output=abcdcdcdcdcdce。

3. 实现

bitarray的实现请参看，下面给出简单的python实现。

# coding=utf-8class LZ77:    """    A simplified implementation of LZ77 algorithm    """    def __init__(self, window_size):        self.window_size = window_size        self.buffer_size = 4    def longest_match(self, data, cursor):        """        find the longest match between in dictionary and lookahead-buffer        """        end_buffer = min(cursor + self.buffer_size, len(data))        p = -1        l = -1        c = ''        for j in range(cursor+1, end_buffer+1):            start_index = max(0, cursor - self.window_size + 1)            substring = data[cursor + 1:j + 1]            for i in range(start_index, cursor+1):                repetition = len(substring) / (cursor - i + 1)                last = len(substring) % (cursor - i + 1)                matchedstring = data[i:cursor + 1] * repetition + data[i:i + last]                if matchedstring == substring and len(substring) > l:                    p = cursor - i + 1                    l = len(substring)                    c = data[j+1]        # unmatched string between the two        if p == -1 and l == -1:            return 0, 0, data[cursor + 1]        return p, l, c    def compress(self, message):        """        compress message        :return: tuples (p, l, c)        """        i = -1        out = []        # the cursor move until it reaches the end of message        while i < len(message)-1:            (p, l, c) = self.longest_match(message, i)            out.append((p, l, c))            i += (l+1)        return out    def decompress(self, compressed):        """        decompress the compressed message        :param compressed: tuples (p, l, c)        :return: decompressed message        """        cursor = -1        out = ''        for (p, l, c) in compressed:            # the initialization            if p == 0 and l == 0:                out += c            elif p >= l:                out += (out[cursor-p+1:cursor+1] + c)            # the repetition of dictionary            elif p < l:                repetition = l / p                last = l % p                out += (out[cursor-p+1:cursor+1] * repetition + out[cursor-p+1:last] + c)            cursor += (l + 1)        return outif __name__ == '__main__':    compressor = LZ77(6)    origin = list('aacaacabcabaaac')    pack = compressor.compress(origin)    unpack = compressor.decompress(pack)    print pack    print unpack    print unpack == 'aacaacabcabaaac'

4. 参考资料

[1] Ziv, Jacob, and Abraham Lempel. "A universal algorithm for sequential data compression." IEEE Transactions on information theory 23.3 (1977): 337-343.

[2] guyb, .